|
2
|
Starke Wechselwirkung und Symmetrie
|
letzte Änderung 17.11.2018
|
|
Oszi-Acht und
Reichweite
|
Um mich der starken Wechselwirkung (kurz sWW) zu nähern, bin ich von der Oszi-Acht aus Kapitel 1 ausgegangen, also dem Zusammenschluss zweier gleicher Oszis zu einer Acht unter Berücksichtigung der Ebene, der Laufrichtung und der Phase.
Eine Acht lässt sich strecken. Da die Schlaufenlänge der Kreiswelle durch ihre Wellenlänge begrenzt ist, muss sie irgendwann reißen. Die Energie, die zum Reißen führt, kann man sich als Spannungsenergie vorstellen, die bis zum Reißen immer weiter anwächst, um sich dann beim Reißen zu entladen.
Für ein primitives Oszi beträgt die maximale Streckung
r = λ/2 - λ/π = λ (1/2 - 1/π) = 0,1816901138162 · λ, d.h. es gilt:
|
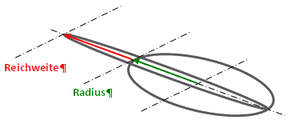
Abb. 2.1:
Reichweite, d.h. bis hierher - und nicht weiter!
|
|
Reichweite der sWW
|
Die Reichweite r = λ (1/2 - 1/π) stellt die obere Grenze für die starke
Wechselwirkung dar, wobei λ die reduzierten Wellenlänge ist.
|
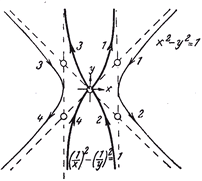 Abb. 2.2: Abb. 2.2:
Die Nummern in Verbindung mit den Pfeilen
zeigen die Bewegung eines Punktes, und wie der
entsprechende Punkt in der transformierten Funktion
im folgt. Spiegelung an den Fixpunten x = ±1 , y = ±1.
|
|
Herleitung der
Dichtefunktion
|
Für die Oszi-Acht gibt es genau zwei Zustände: ist Acht, ist keine mehr. Dies legt deren wahrscheinlichkeitstheoretische Deutung nach Bernoulli nahe. Es wird also eine Dichtefunktion f(x) über die Reichweite r gesucht, die die sWW möglichst korrekt beschreibt. Sie wird so normiert, dass auf der x-Achse die Reichweite r auf die 1 fällt.
|
|
|
Über die Dichtefunktion f(x) lässt sich noch mehr sagen:
- Sie ist im Intervall 0 < x < 1 stetig (notwendig für eine Dichtefunktion)
- Für x → 1, muss f(x) → ∞ gegen (definitives Reißen an der Stelle)
- f'(+0) muss möglichst groß sein (linksseitige Ableitung an der Stelle 0)
- Es ist zu vermuten, dass f(x) einen quadratischen Term enthält
- In den Grenzen von 0 bis 1 muss ∫f(x) = 1 sein
Soll ein quadratischer Anstieg auf engstem Raum passieren, so muss die Funktion den Term (1/x)² beinhalten. In Frage kommt damit die folgende Funktion:
|
|
Dichtefunktion der sWW
|
(1/x)2 - (1/y)2 = 1 definiert die Dichtefunktion y = f(x) der sWW für 0 < x < 1.
|
|
|
Die Dichtefunktion ist bei 0 nur links- und bei 1 (Polstelle) nur rechtsseitige stetig. Seine Integrationsgrenzen liegen also im offenen Intervall ]0,1[, was folgende Aussage erlaubt:
- Die absolute Stabilität gibt es physikalisch nicht!
|
|
|
Eindeutigkeit
|
Warum soll genau dies die Dichtefunktion der sWW sein? Begründen lässt sich dies damit, dass die Stabilität keine reale Größe sein kann. Neben allen anderen Forderungen, erfüllt die obige Dichtefunktion auch diese Forderung:
|
|
|
|
Die Sinusfunktion lässt sich durch Koordinatentransformation über die Abwicklung des Einheitskreises herleiten. Ein Punkt auf der Kreislinie folgt dann der Sinusfunktion. Abb. 2.2 zeigt dies analog für einen Punkt, der sich auf der Einheitshyperbel bewegt. Um mittels Transformation von der Kreis- zur Hyperbelfunktion zu gelangen, ist der Zahlenraum auf die komplexen Zahlen zu erweitern - was zu zeigen war.
|
Einheitskreis: x² + y² = 1
Die angestellte Überlegung geht von der als Kreiswelle
im primitiven Oszi aus!
|
|
absolute Schärfe
der Reichweite
|
Die Funktion ist trotz der ausgelassenen Polstelle bei 1 eine Dichtefunktion, denn ihre Integration ergibt als Grenzwert 1. Konsequenz der Polstelle ist die absolute Schärfe der Reichweite, was der physikalischen Beobachtung entspricht.
|
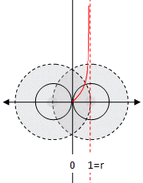
Abb. 2.3a:
obere = untere Grenze = 0
Entspannte Situation - solange
wie sich keiner bewegt!
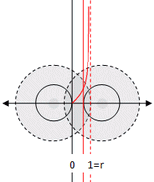
Abb. 2.3b:
obere Grenze = rote
durchgezogene Linie
Ursache für die Spannung
ist immer der andere!
|
|
Energiedichte-
funktion
|
Wird der Maßstab der x-Achse so geändert, dass die 1 bei r liegt,
so ergibt sich die zugehörende Energiedichtefunktion (r/x)² - (r/y)² = 1.
Mit x = r als obere Grenze ergibt die Lösung des Integrals r².
|
|
Bindung über
Oszi-Achten
|
Bei den Achten handelt es sich um identische Oszis in einer Ebene. Aufgrund ihrer Wirkungsweise ist die Dichtefunktion vom Oszi-Kreis nach außen aufzutragen. Dabei sollen die Oszi-Kreise schon innerhalb ihrer Reichweite liegen, denn nur dann ist die sWW wirksam - siehe Abb. 2.3a und b.
|
|
Abbildung 2.3a
|
Da in diesem Fall die sWW = 0 ist, sind die beiden folgenden Zustände
nicht zu unterscheiden: Die Oszi-Acht ist geschlossen - oder offen.
|
|
Abbildung 2.3b
|
Die obere Integrationsgrenze wird durch den jeweils anderen Oszi-Kreis bestimm. Damit wird die sWW erst in dem Moment für das Oszi wirksam, wenn der, um die Reichweite r erweiterter Kreis, von der Bahn des anderen Oszis geschnitten wird.
|
|
Multiplikationssatz
|
Der Multiplikationssatz der Wahrscheinlichkeitstheorie soll zur Bestimmung der Bindungsenergie in einer Oszi-Acht genutzt werden. Multiplikation bedeutet in dem Fall Quadrierung. Notwendige Voraussetzung ist die wahrscheinlichkeitstheoretische Unabhängigkeit der beteiligten Ereignisse. Die ist mit dem Dilemma der QT gegeben - siehe Kapitel 1.
|
|
|
Die Stärke der sWW nach dem Zerreißen ist bekannt. Sie entspricht dem Integral über die Dichtefunktion in den passenden Grenzen - siehe Abb. 2.3b. Nach dem Multiplikationssatz entspricht dies dem Quadrat der Stärke vor dem Zerreißen. Anders herum formuliert ergibt sich der folgende Satz:
|
|
Satz 2.1
Multiplikationssatz
|
Die Stärke der sWW einer Oszi-Acht entspricht der Wurzel des Integrals,
das sich in Bezug auf die einzelne Kreiswelle ergibt!
|
|
|
|
Wenn Satz 2.1 für die Funktion der Energiedichte gilt, so gilt dies natürlich auch für die Funktion der Wahrscheinlichkeitsdichte. Da Wahrscheinlichkeiten ≤ 1 sind, wird die Wahrscheinlichkeit durch das Ziehen der Wurzel größer (trivial).
|
|
|
Verallgemeinerung
|
Wenn keine Eigenschaften des anderen Oszi eine Rolle spielen darf, müssen die Kreiswellen nicht die gleiche Wellenlänge haben, und noch nicht einmal in der gleichen Ebene liegen. Dies führt zu folgender Verallgemeinerung:
|
|
|
Satz 2.2
Satz der sWW
|
Die Stärke der sWW wird nur durch den Durchstoß der zweiten Kreiselle
innerhalb der Reichweite der ersten Kreiswelle bestimmt.
Der Durchstoßpunkt bestimmt die Obergrenze des Integrals über die Energiedichtefunktion, und damit die Größenordnung der sWW.
|
In der Ebene ist der Durchstoßpunkt mit dem Punkt
des kürzesten Abstandes gleichzusetzen!
|
|
|
Solange der Durchstoßpunkt erhalten bleibt, spielt damit die räumliche Lage der Kreiswellen bei der Bestimmung der sWW keine Rolle, und da die Reichweite ebenso nach innen abgetragen werden kann, gilt:
|
|
|
Korollar 2.2
|
Up- und Down-Oszi zentrieren sich gegenseitig!
|
|
|
Dipolwelle
und sWW
|
Das Dilemma der QT verbietet nicht die Wechselwirkung einer Kreiswelle mit sich selbst. Dazu sollte es kommen, wenn zwei sich im Kreis gegenüberliegende Punkte näher als die Reichweite kommen, was bei der Dipolwelle der Fall ist. Dass sie in diesem Fall mit keiner anderen Welle mehr in starke Wechselwirkung treten kann, wird erst mit dem Vertauschungsphänomen gezeigt.
|
|
|
|
|
|
|
2.1
|
Vertauschungsphänomen und Symmetrie
|
letzte Änderung 17.11.2018
|
|
sWW und
Vertauschung
|
Up- und Down-Oszi sind schon sehr speziell, denn mit
Eu und Ed für die Energie der Kreiswellen, und mit
ru und rd für die entsprechenden Reichweiten, ist
Eu/rd = Ed/ru = 4,00971403630627 104 kgm/s² = v.
Die Konstante v sein der Vertauschungsfaktor.
|
|
|
|
rd² bzw. ru² sind die Lösungen des Integrals über die entsprechende
Energiedichtefunktion über die gesamte Reichweite.
1/rd und 1/ru sind dann die Normierungsfaktoren.
Wd und Wu sind damit die maximale Spannungsenergie der entsprechenden Oszis.
In Verbindung mit der Ausgangsgleichung ergibt sich ein Phänomen:
|
|
|
Das Vertauschungs-
phänomen
|
Bei den Kreiswellen der Up- und Down-Oszis entspricht die maximale
Spannungsenergie der sWW jeweils der Kreiswellenenergie des anderen Oszis!
|
|
|
|
Dies kann nur alternativ gemeint sein, denn die wahrscheinlichkeitstheoretische Herleitung aus einem System, das nur zwei Zustände erlaubt, toleriert keine Vermischung von Zuständen. Damit bleibt nur noch eine Interpretation übrig:
|
wichtiger Schluss!
|
|
|
- Das Vertauschungsphänomen beinhalte, dass eine Vertauschung
niemals gleichzeitig in beiden Richtungen ablaufen kann!
|
Das Vertauschungsphänomen bewirkt den gleichen
Effekt wie das Austauschteilchen aus der Standardtheorie!
|
|
|
Von gleichzeitig darf eigentlich nicht die Rede sein, denn im Raum der starke WW gibt es die Zeit nicht (Bernoulli). Zu dem gedanklichen Problem kommt es, da jede der beiden anderen Wechselwirkungen einen Raum voraussetzt, dessen vierte Dimension die Zeit ist. Aufgrund ihrer Unverträglichkeit erfordert dies ihre Separation. Die übernimmt der zeitlose Wahrscheinlichkeitsraum.
|
Die TO benötigt keine Austauschteilchen!
wurde bereits in Kapitel 0 thematisiert
|
|
|
Im nächsten Kapitel zeigt sich, dass innerhalb der Reichweite der sWW die Unschärferelation gilt. Dies legt nahe, dass sie im Zusammenhang zur Separation über den Wahrscheinlichkeitsraum steht.
|
- siehe letzter Absatz "John von Neumann" in Kapitel 2.2
|
|
Bindungsparadoxon
|
Das Vertauschungsphänomen führt bei der Bindung von zwei Protonen und zwei Neutronen zu einem interessanten Ergebnis. Da jeweils alle drei Oszi-Achten an der Bindung beteiligt sind, lassen sich folgende Energiegleichungen aufstellen:
P≡P: 4Wu + 2Wd = 4Ed + 2Eu = 2 · Kreiswellenenergie des Neutrons (u + 2d)
N≡N: 4Wd + 2Wu = 4Eu + 2Ed = 2 · Kreiswellenenergie des Protons (2u + d)
Eine ausgeglichene Energiebilanz ergibt sich somit erst mit dem Heliumkern!
|
|
|
Austauschsequenzen
|
Schaltet man zwischen zwei Up-Oszis ein Down-Oszi wie im Proton, bzw. zwischen zwei Down-Oszis ein Up-Oszi wie im Neutron, so ergeben sich folgende Sequenzen:
|
|
|
|
|
Proton
|
Neutron
|
|
Eu – Wd|Ed – Wu
|
Ed – Wu|Eu – Wd
|
|
|
In der Standardtheorie kommt es mit den 3 Farbladungen
zu 9 möglichen Kombinationen, was eine zu viel ist!
|
|
|
Da beim direkten Austausch die Energien nicht passen, bleibt es dabei.
Unter Beachtung der Reihenfolge ergeben sich 4 mögliche Vertauschungen und 4 weitere, da die beiden Up-Oszis im Proton und beiden Down-Oszis im Neutron aufgrund ihre Phasenverschiebung zu unterscheiden sind - also insgesamt 8.
Die Dipolwellen bleiben unberücksichtigt, da es dort zur sWW mit sich selbst gekommen ist (zusammengefallene Faltdipole).
|
8 Kombinationen und keine Farbladungen in der TO!
|
|
geometrische
Symmetrie
|
Ausgehend von der arithmetischen Symmetrie in Kapitel 1,
ergibt sich die geometrische Symmetrie:
Mit den bekannten Massen von Proton und Neutron ist
Es = 5,01509060622476 10-11 kgm²/s² die arithmetische Symmetrieenergie,
und ΔEs = 8,18710506545916 10-14 kgm²/s² die Störung durch das Elektron.
|
Verallgemeinerung der geometrischen Symmetrie
zur “allgemeinen Symmetrie” - siehe Ende Kapitel 2.2
|
|
|
Damit ist Ed2 + Eu2 = 2,89436769763191 10-21 (kgm²/s²)², und
S = 5,01509728892004 10-11 kgm²/s² die geometrische Symmetrieenergie.
Mit den Binomischen Formeln gilt nach dem Ausklammern und Kürzen von 2:
Dies reicht nun aus, um die Berechnung umzukehren.
|
|
|
Symmetrie der
Up- und Down-Oszis
|
Das Paar von Up- und Down-Oszi lässt sich aus der geometrischen
Symmetrieenergie und der Störung um + bzw. - eine Elektronmasse bestimmen!
|
|
|
|
Rechnerisch ergeben sich für das Up- und Down-Oszi so folgende Massen:
mu = 5,57093146121995 10-28 kg, md = 5,58915022703995 10-28 kg
Über die Strukturformeln ergibt sich die Gesamtmasse von Proton und Neutron, wobei die Nukleonen als zusammengesetzte Quantenobjekte einen Massendefekt aufgrund ihrer Bindungsenergien zeigen.
|
|
|
Aufteilung
Massendefekte
|
|
Masse in kg
|
Proton (2u+d)
|
Neutron (u+2d)
|
|
nach Strukturformel
|
1,67310131494798 10-27
|
1,67492319152998 10-27
|
|
plus Massendefekt
|
-4,79537947984654 10-31
|
4,15947001511464 10-33
|
|
gleich Gesamtmasse
|
1,672621777 10-27
|
1,674927351 10-27
|
|
|
Massendefekt - siehe Kapitel 1.2
|
|
sWW und
Massendefekt
|
Die obige Tabelle zeigt die Massendefekte, die sich in Kapitel 1 über den β-Zerfall ergeben haben. Es stellt sich nun die Frage, ist Ihre Berechnung jetzt auch über die sWW möglich?
|
- siehe nachfolgende Kapitel
|
|
|
|
|
|
2.2
|
Exzentrizität, Unschärfe und Normierung
|
letzte Änderung 23.04.2018
|
|
Massendefekt
und Exzentrizität
|
Im Proton bzw. Neutron bilden die Kreiswellen der Up- und Oszis Schalen. Bei den Schalen sorgt die sWW für ihre Zentrierung, und zwar um so stärker, je mehr andere Effekte dem entgegenwirken. Die dadurch verursachten Massendefekte lassen sich über die Energiedichtefunktion berechnen.
|
|
|
|
In den Abbildungen 2.3a und 2.3b vom Anfang des Kapitels 2 ist zu sehen, wie die Energiedichtefunktion für den Fall aufzutragen ist, dass die eine Kreiswelle außerhalb der anderen liegt. Die Dichtefunktion ist über der Verbindungslinie der Kreismittelpunkte aufzutragen, denn auf dieser Linie ist die Entfernung der Kreislinien minimal, womit auch der Energiezuwachs minimal ausfällt.
|
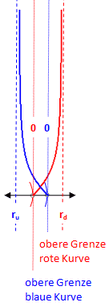
Abb. 2.2.1:
Je besser zentriert,
je geringer die Rückstellkraft!
ru = Reichweite des Up-Oszis
rd = Reichweiten des Down-Oszis
|
|
Zentrierung
|
Verschieben sich zusammenfallende Kreismittelpunkte, so lassen sie durch eine Gerade verbinden. , die durch beide Mittelpunkte geht. Sind beide Oszis zentriert, so fallen beide Mittelpunkte zusammen, womit jede Gerade durch den Punkt erlaubt ist. Die minimale Entfernung der Kreislinien ist in diesem Fall gleichzeitig auch die maximale.
Bei ineinander liegenden Kreiswellen ist die Dichtefunktion vom äußeren Kreis nach innen abzutragen. Erlaubt ist dies, da der Ausgangspunkt der Reichweite, und somit auch der Dichtefunktion, die Kreislinie bleibt - siehe Abb. 2.2.1 rechts. In der Abbildung entspricht der Abstand der Nulllinien der Obergrenze im Integral über die Dichtefunktion.
Seien du und dd die Durchmesser des Up- und Down-Oszis, so ist
bei Zentrierung der Abstand der Nulllinien (du - dd)/2 (siehe rechts).
|
|
Vorzeichenwechsel
|
Liegen die Kreiswelle getrennt, so führt die sWW zu einem Energiezuwachs. Bei ineinander liegenden Kreiswellen bewirkt das einmalige Umklappen der Dichtefunktion nach innen einen Vorzeichenwechsel. Physikalisch ist dies als Massendefekt zu interpretieren.
|
Massendefekt negativ!
|
|
Exzentrizität
|
Falls Kreise nicht zentriert sind, so lassen sie sich durch eine Gerade verbinden, womit sich zwei mögliche Berechnungen der sWW ergeben. Die eine bezieht sich auf den verringerten, die andere auf den entsprechend vergrößerten Abstand der Kreislinien. Dass nur eine Berechnung stimmen kann, wird dann besonders einsichtig, wenn der ein Kreis von innen am anderen liegt.
|
|
|
|
Bei minimalem Abstand fallen Unter- und Obergrenze des Integrals zusammen, womit es 0 ist, und keine Zentrierung stattfindet.
|
Verschiebung um Δx = (du - dd)/2
Integration von 0 bis 0 , bzw. von 0 bis du - dd
|
|
|
Physikalisch kommt nur der maximale Abstand in Betracht, da sich darüber die Energiebilanz des Gesamtsystems minimieren lässt (Massendefekt negativ).
|
|
|
statisch
|
Ist die Exzentrizität durch Bindungskräfte und Achten-Bildung verursacht,
so geht es um eine rein geometrische Exzentrizität, die also statisch ist.
|
|
|
dynamisch
|
Exzentrizität entsteht auch durch Anregung. Die Schrödingergleichung beschreibt im Quantenmaßstab die Energiespeicherung aufgrund von Bewegung. Danach wird bei der Bewegung eines Teilchens, zwischen Translation, Rotation und Vibration unterschieden. Überträgt man dieses auf das Oszi-Modell, so führt dies zu folgender Entsprechung:
|
|
|
|
Die Stärke der Vibration entspricht einer bestimmten Exzentrizität,
die in de TO dynamische Exzentrizität heißen soll.
Ihre Berechnung erfolgt damit genauso wie bei statischer Exzentrizität.
|
Einfacher geht es nicht!
|
|
angeregtes Proton
|
Regt man ein Proton an, so müsste sich die Anregungsenergie theoretisch auf die Bewegung der Schwerpunkte der drei Quarks restlos verteilen (2u+d).
- Experimentell zeigt sich jedoch, dass nur 30-50% der Anregungsenergie in der Bewegung der Schwerpunkte stecken.
Ein Vergleich der klassischen Bewegungsgleichung mit den kumulierten Werten der Energiedichtefunktion zeigt, dass dies zu einer viel geringeren Auslenkung der Schwerpunkte führt. In der TO passt also die Vorhersage!
|
Um die Ergebnisse des Experimentes "angeregtes Proton"
zu erklären, werden im SM die Seequarks eingeführt!
|
|
Die TO liefert auch so das richtige Ergebnis!
|
|
Unschärferelation
|
In der TO kann ein Zusammenhang zur Exzentrizität hergestellt werden.
σx σp ≥ ħ/2 ist die Streuungsvariante der Unschärferelation.
σx kann direkt mit der Exzentrizität der Oszis gleichgesetzt werden.
σp ist wie gewohnt die Standardabweichung des Impulses.
|
|
|
|
Die Unschärfe ist damit direkt an die starke Wechselwirkung gebunden, und da die sWW auf die Reichweite beschränkt ist, gilt dies auch für Unschärferelation.
|
Einstein hat die Allgemeingültigkeit
der Unschärferelation immer angezweifelt.
|
|
Satz 2.2.1
|
Die Unschärferelation gilt in der TO nur innerhalb der Reichweite der sWW!
|
|
|
Unschärfe und
Energiegeleichung
|
Der in Bezug auf die Unschärferelation relevante Term ist rot umrandet.
Bei der Herleitung der Energiegleichung als Linearkombination aus h undħ, war klar, dass beim zweiten Term der Faktor 2 sein muss, denn erst mit mal 2 ist die rechte Seite der Unschärferelation ein ganzes Quant.
|
|
|
Nullpunktsfluktuation
|
Sie ist bislang experimentell nicht zweifelsfrei nachzuweisen. Theoretisch wird ihre Existenz mit der Unschärferelation begründet. Die gilt in der TO jedoch nur innerhalb der Reichweite der sWW, und da deren Energie aufgrund ihrer wahrscheinlichkeits- theoretischen Herleitung immer positiv ist, kann es in ihrem Gültigkeitsbereich keine Auslöschung, also auch keine Nullpunktsfluktuation geben.
|
Ein gefundenes Fressen für alle Esoteriker!
|
|
Satz 2.2.2
|
Die Nullpunktsfluktuation aufgrund der Unschärferelation gibt es in der TO nicht!
|
|
|
Berechnung
der Symmetrie
|
Mit Hilfe des Vertauschungsphänomens lassen sich weitere Zusammenhänge aufklären. Die nachfolgende Exceltabelle hilft dabei, die Übersicht zu behalten.
|
|