|
1
|
Oszi und Schalenmodell
|
letzte Änderung 02.04.2019
|
|
|
|
|
|
1.1
|
Das Oszi
|
letzte Änderung 02.04.2019
|
|
Energiegleichung
des Photons
|
Nach dem Standardmodell ist das Photon nur ein Quasiteilchen, da es sich definitiv um eine elektromagnetische Welle handelt,
für welche die Plancksche Energiegleichung E = h ν gilt,
wobei ν die Frequenz, und h das Plancksche Wirkungsquantum ist.
|
Lichtquantenhypothese von Albert Einstein (1905)
|
|
Quantenhypothese
des Oszi
|
Über das Plancksche Wirkungsquantum hinaus kommt dem reduzierten Planckschen Wirkungsquantum ħ quantenphysikalische Bedeutung zu.
|
ħ = h/2π
|
|
|
Mit h und ħ wird nun die einfachste Linearkombination gebildet, deren Faktor bei ħ ganzzahlig ist. Letzteres ist notwendig, wenn die Heisenbergsche Unschärferelation stimmen soll - siehe Kapitel 2.2.
Soll sich die Linearkombination wieder als Wirkungsquantum schreiben lassen, so muss sich die Frequenz bzw. die Wellenlänge ausklammern lassen.
|
 siehe auch Kapitel 0.2 siehe auch Kapitel 0.2
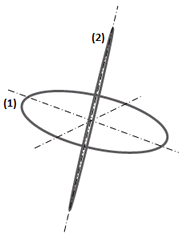
Abb. 1.1.1:
primitives Oszi
Bei einer Windung der Kreiswelle, wenn also λ
gleich dem Umfang ist, sei das Oszi primitiv.
|
|
Energiegleichung
des Oszi
|
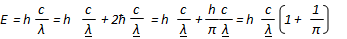
|
|
|
Im einfachsten Fall lässt sich die Gleichung wie folgt deuten:
Steht der erste Term für eine Kreiswelle mit dem Umfang λ (1), so
steht der zweite Term für den passenden Faltdipol mit der Länge λ/2 (2).
|
|
Entwicklung
der Theorie
|
Soll es eine "Theorie der Oszis" (TO) geben, so muss jeder der obigen Terme Quant im Sinne des Dilemmas der QT sein, denn ansonsten würde es sich um quantentheoretischen Unsinn handeln! Die TO entwickelt sich entlang dieser Forderung, und zwar über alle Wechselwirken hinweg - siehe auch Kapitel 0.2.
Hier geht es zunächst um die elektromagnetische Wechselwirkung
In Kapitel 2 geht es um die starke Wechselwirkung.
In Kapitel 3 geht es um die gravitaive Wechselwirkung.
Die schwache Wechselwirkung ist Sache der Dipolwelle.
|
|
wie sinnvoll
ist der Ansatz?
|
Aufgrund der linken Seite in der Energiegleichung des Oszi, die nichts anderes als die Plancksche Energiegleichung darstellt, ist die Erzeugung und Vernichtung von Teilchen zumindest formelmäßig klar. Die spontane Emission von Licht wird mit der starken Wechselwirkung in Kapitel 2 verstanden. Zu einer echten Quantentheorie wie rechts beschrieben, wird die TO erst, wenn sie vollständig ist (Kapitel 3), denn dann erlaubt sie die Vorhersage der Elementarteilchen.
Es soll nun weiter untersucht werden, wie sinnvoll dieses Stringmodell ist.
|
Das Standardmodell ist keine echte Quantentheorie in dem Sinne, dass die Existenz von Teilchen angenommen wird. Im Besonderen kann es die Erzeugung oder Vernichtung von Teilchen nicht erklären. Zudem bleibt die spontane Emission von Licht unverstanden.
|
|
Probleme, die es in der TO nicht gibt!
|
|
relativistische
Invarianz der Oszis
|
Die Geometrie eines Oszis definiert sich über die Ausbreitungslinie der elektromagnetischen Wellen. Die lassen sich beim Oszi aus der Kreiswelle entwickeln. Zusammen mit der relativistischen Invarianz der Elektrodynamik erlaubt dies ihre Reduzierung auf die Geometrie. Es ist also nur noch zu zeigen, dass ihre Geometrie bei relativistischen Geschwindigkeiten erhalten bleibt (Lorentz-Invarianz). Dies ist der Fall, wenn ihre Transformationen im Minkowski-Raum Elemente der eigentlichen Lorentz-Gruppe SO(3,1) sind. Dazu reicht es, dass die Abbildungen ihrer Geometrie auf sich selbst zur Drehgruppe SO(3) gehören. Bei den primitiven Oszis ist dies aufgrund ihrer Drehsymmetrie gegeben. Nach Kapitel 3 sind die Neutrinos und Leptonen als Oszis nicht primitiv. Da sich ihre Geometrie durch Drehung und Spiegelung in sich selbst überführen lässt, gehören sie auch dazu. Zusammenfassend gilt:
|
gehört zu den Standardwerkzeug in der Quantenphysik
|
|
Satz 1.1.1
|
Ein Oszi, bzw. ein Quantenobjekt aus Oszis, bleibt aufgrund der Invarianz seiner Geometrie auch bei relativistischer Geschwindigkeit immer das gleiche Teilchen!
|
Lorentz-Invarianz von Quantenobjekten aus Oszis!
|
|
relativistische
Massenzunahme
|
Da nach dem letzten Satz ein Oszi seine Geometrie auch bei relativistischer Geschwindigkeit nicht ändert, kann dieser Effekt nicht funktional von der Geometrie abhängen. Anders gesagt:
|
|
|
Korollar 1.1.2
|
Ein Oszi kann aufgrund seiner invarianten Geometrie nicht direkt für
seine relativistische Massenzunahme verantwortlich gemacht werden.
|
|
|
Rückgriff auf
Kapitel 0
|
Zur Erinnerung: Selbstverständlich muss das Oszi den beiden Feldtheorien gehorchen. Dies betrifft seine Bewegung in Feld, und damit letztlich seine Geometrie als Objekt aus Strings. Andererseits lassen sie sich nach dem Dilemma der QT in keiner ihrer Eigenschaften von einem anderen String abhängig machen, was eine direkte Wechselwirkung ausschließt.
|
Elektromagnetische Feldtheorie (EMF) und ART
werden so benutzt, wie sie jeder kennt!
|
|
|
Jede Verzerrung der Geometrie des Oszis führt zu einer zusätzlichen Bindungsenergie, deren Ursache eine der Wechselwirkungen ist. Aufgabe der TO ist es, die Geometrien zu finden, die energetisch mindestens ein lokales Minimum aufweist. Die verschiedenen Symmetrien helfen dabei ebenso wie die Tatsache, dass nur bestimmte Aspekte der Geometrie relevant sind (Vergissfunktor).
|
Eine Wechselwirkung ist nur indirekt
über die Geometrie des Strings möglich!
|
|
|
Die Vorhersage der TO hat entscheidenden Anteil daran, dass die Berechnung der Elementarteilchen überhaupt gelingen kann. Nach ihr dürfen Kreis- und Dipolwelle als entkoppelt angesehen werden. Dies betrifft die elektromagnetische und die gravitative Wechselwirkung. Da die Berechnungen immer vom primitiven Oszi ausgehen, interessiert die geometrische Konsequenz, die dies hat, denn die ist umgekehrt zu beachten - siehe nachfolgenden Satz:
|
Vorhersage der TO, siehe Kapitel 0.2
- siehe auch “Synchronitätsphänomen” in Kapitel 3.1
|
|
Satz 1.1.3
|
Kreis- und Dipolwelle können als elektromagnetisch und gravitativ entkoppelt
angesehen werden, solange die Kreiswelle im Oszi in ihrer Ebene bleibt!
|
|
|
|
Die Dipolwelle kann im obigen Satz unerwähnt bleiben, denn es wird sich herausstellen, dass sich ihre Geometrie an der Kreiswelle orientiert. Die Einschränkung auf die Ebene in obigem Satz, ist plausibel und notwendig. Es wird sich zeigen, dass die Leptonen diese Einschränkung aufgrund ihrer Wicklungsart verletzen. Beim Elektron, Myon und Tauon äußert sich dies durch ihre magnetische Anomalie. Allgemein, also auch bei nicht primitiven Oszis bleibt obiger Satz nur gültig, wenn die Ebene nicht mehr die euklidische Ebene ist. Grund ist die Raumzeitkrümmung aus der ART, die durchschlägt!
Als Folgerung aus der Symmetrie des primitiven Oszis ergibt sich:
|
Eine Ebene ist in der TO nicht zwingend euklidisch eben,
was aber beim primitiven Oszi noch ignoriert werden darf!
|
|
Korollar 1.1.4
|
Vom primitiven Oszi gibt es kein Anti-Oszi.
|
|
|
|
Zusammenfassend ist festzuhalten:
|
|
|
Satz 1.1.5
|
Im primitiven Oszi liegt das E-Feld in der Ebene der Kreiswelle, das B-Feld in der Ebene,
in der sich der Dipol faltet, und beide Felder stehen orthogonal aufeinander.
|
|
|
|
Das E- und B-Feld als orthogonal anzunehmen, ist in einem ungestörten Quantensystem nicht nur naheliegend, sondern aus Symmetriegründen sogar zwingend. Die Feldorientierung lässt sich über das Ausschlussprinzip bestimmen. Die Felder der Wellen interagieren in jedem Fall. Netterweise weisen die Maxwell-Gleichungen eine Asymmetrie auf. Damit reicht es, sich zu überlegen, welche Feldorientierung die Drehsymmetrie nicht verletzt. Dies läuft auf die Kombination hinaus, bei der die Dipolwelle nicht gleich kippen will, also die obige!
|
die Vorhersage der TO erzwingt Symmetrie!
|
|
|
Wem dieser Argumentation unzureichend erscheint, kann auch wie folgt argumentieren: Die Quantenzahlen, die sich mit den Integrationsregeln leicht nachrechen lassen, müssen stimmen. Die stimmen aber nur bei obiger Feldorientierung - siehe nächstes Kapitel. Mit der Eindeutigkeit der Quantentheorie und der Tatsache, dass die Quantenzahlen der klassischen Quantenmechanik verifiziert wurden, ist dies ein Beweis.
|
Achtung, die Abweichung beim Spin um den Faktor ½
ist nur der Definition geschuldet!die
|
|
|
|
|
|
1.2
|
Das Up- und Down-Oszi
|
letzte Änderung 26.01.2018
|
|
|
Damit der Beitrag nachvollziehbar bleibt, sei aufgeführt, was unter welchen Annahmen und Voraussetzungen gezeigt wird - siehe Punkt 1 und 2.
|
|
|
Punkt 1
|
Sind Up- und Down-Oszi primitive Oszis, die entsprechend den bekannten Strukturformeln für die Up- und Down-Quarks die Nukleonen bilden sollen, so ergibt sich allein unter der Voraussetzung, dass Ladung und Spin stimmen sollen, ein geometrisch eineindeutiges Schalenmodell.
|
Nukleonen wie eine Zwiebel? Ein Protonenbeschleuniger des Argonne National Laboratory lieferte bereits in den 1960-gern Messwerte, die diese Hypothese nahelegte.
|
|
|
- Aufgrund der Eineindeutigkeit des Schalenmodells von Proton
und Neutron sind damit auch die Strukturformeln bestätigt!
|
Anscheinend ein unerwüschtes Ergebnis!
|
|
Punkt 2
|
Um Up- und Down-Oszi eineindeutig zu bestimmen, fehlt ihre Wellenlänge, also ihre Energie. Die wird zunächst aus den bekannten Massen von Proton und Neutron bestimmt. Da zusätzlich der β-Zerfall benutzt werden muss, um die Berechnung abschließen zu könne, geht auch noch die Masse des Elektrons ein.
|
|
|
Ladung und Spin
|
Um die beiden Punkte angehen zu können, muss zunächst einmal geklärt werden, was Ladung und Spin der TO bedeuten.
|
|
|
Definition 1.2.1
|
Die Quantenzahl des Oszi soll sich auf den ersten Term in seiner Energiegleichung beziehen.
Sie sei der Wert des Intergral ¼ sin(s), wobei s das Bogenmaß über eine Periode darstellt.
Bei der Integration über das E-Feld, geht es um die Ladung.
Bei der Integration über das B-Feld, geht es um den Spin.
|
Festlegung rein mathematisch!
Was sich hinter dem Spin verbirgt, klärt sich später.
|
|
|
- Die Definition vom Spin wurde analog zur Ladung vorgenommen!
Beim Oszi ist die Quantenzahl vektoriell zu ermitteln:
Der Betrag ergibt sich durch Integration im Kreis rechts herum:
Das Vorzeichen der einzelnen Flächenvektoren ist das Produkt der Vorzeichen aus Flächenorientierung* und Amplitude. Die einzelnen Flächenvektoren greifen im Flächenschwerpunkt an - siehe Skizze rechts. Zur vektoriellen Addition dürfen die einzelnen Vektoren auf der gemeinsamen Symmetrielinie verschoben werden.
* Schulmathematik: Läuft man über die x-Achse um die Fläche links herum,
so ist ihr Wert positiv, und umgekehrt.
Die Integration der Kreiswelle erfolgt von innen gesehen rechts herum (= +).
Die Integration der Dipolwelle erfolgt von außen gesehen.
|
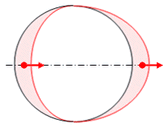 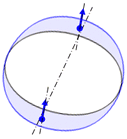
Abb. 1.2.1a und b:
Das E-Feld ist rot, und das B-Feld blau!
|
|
|
Bei dieser Vorgehensweise ergibt sich für ein primitives Oszi:
Ladung Kreiswelle = 1, Spin Kreiswelle = 1
Ladung Dipolwelle = 0, Spin Dipolwelle = 0 (eigentlich nicht definiert)
- Bei der Überprüfung der Quantenzahlen kann also die Dipolwelle,
da sie keinen Beitrag liefert, unberücksichtigt bleiben!
|
Die Integration im Kreise herum gestaltet
sich nur bei den primitiven Oszis so einfach.
|
|
Ladung und Spin
des Photons
|
Die Festlegung auf die obigen Rechenregeln zur Bestimmung der Quantenzahlen sollte auch bei Photon schlüssig bleiben.
Wird der Kreisumfang in der Abb. 1.2.1a an einem der Nulldurchgänge aufgetrennt, so lässt sich die Welle in der Zeichenebene abrollen, womit die roten Pfeile in die entgegengesetzte Richtung zeigen. Mit ihrer vektoriellen Addition wird die Ladung des Photons 0.
Die Abb. 1.2.1b liegt auf der Oberfläche eines Zylinders. Die lässt sich, an einem der Nulldurchgänge der Länge nach auftrennen, und in der Ebene ausbreiten, wobei die Richtung der blauen Pfeile erhalten bleibt. Mit ihrer vektoriellen Addition wird der Spin des Photons 1.
|
Abweichungen in den Quantenzahlen
zur klassischen QT interessieren solange nicht,
wie das Gesamtsystem schlüssig bleibt!
|
|
zu Punkt 1
|
Es ist zu überlegen, wie die Kreiswellen, die um einen gemeinsamen Mittelpunkt drehen sollen, zueinander anzuordnen sind, dass sich die richtigen Quantenzahlen ergeben. Dass ihnen nichts anderes übrig bleibt, als um einen gemeinsamen Mittelpunkt zu drehen, zeigt sich in Kapitel 2.2.
|
Schalenmodell
|
|
Ladung
|
Zunächst geht es darum, inwieweit die Einhaltung der korrekten Ladung die Freiheitsgrade der Oszi-Kreiswellen eingeschränkt.
|
|
|
Proton
Ladung +1
|
Angenommen eines der Up-Oszis sei gegenüber dem anderen um 180° gedreht, so löschen sich die elektrischen Felder gegenseitig aus, womit die Ladung zusammen 0 ergibt. Damit wäre allein das Down-Oszi für die Ladung +1 des Protons verantwortlich, und seine Rotationsebene wäre somit völlig frei.
Mit der obigen Annahme ergibt sich zwar eine Lösung, die aber nicht die einzige sein muss! Deshalb wird nun angenommen, dass das Down-Oszi nicht allein für die Ladung verantwortlich sei. Benutzt man zur Bestimmung der Ladung die vektorielle Addition, so führt jedes Kippen der einen Up-Oszi Ebene aus der Ebene des anderen Up-Oszis zu einer Resultierenden ungleich 0, womit die Gesamtladung ungleich 1 wird. Folglich ist die erste Annahme die einzige Lösung.
|
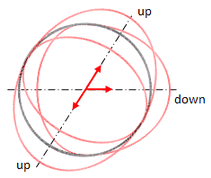
Abb. 1.2.2a
Ladung Proton = 1
Drehen des Down-Oszis um seine Symmetrieachse erlaubt!
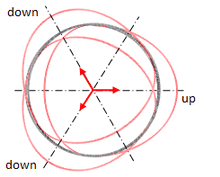
Abb. 1.2.2b
Ladung Neutron = 0
Drehen der Oszis um ihre Symmetrieachsen erlaubt!
|
|
Satz 1.2.2
|
Im Proton ist die Schale des Down-Oszis frei in der Rotation bezogen auf die Schale, der gegenläufig in einer Kreisebene orientierten Up-Oszis.
Das Down-Oszi bestimmt damit allein die Ladung des Protons = 1!
|
|
Neutron
Ladung 0
|
Alle 3 Oszis weisen eine Phasenverschiebung von 2/3 π gegeneinander auf. Trägt man alle 3 E-Quants entsprechend ihrer Phasenverschiebung über den Umfang des Oszi-Kreises auf, so ist deren vektorielle Ladungssumme immer 0.
|
|
Satz 1.2.3
|
Im Neutron sind die drei Symmetrieachsen der Oszis in der Ebene symmetrisch angeordnet, d.h. der eingeschlossene Winkel beträgt 120°.
Damit ist die Gesamtladung im Neutron = 0!
|
|
|
Dies muss so sein, da sich 3 gleichlange Vektoren nur dann in der Ebene zu 0 addieren können, wenn sie ein gleichseitiges Dreieck bilden.
Für jedes der drei Oszis lässt sich in Bezug auf den über den Umlauf abgetragenen Sinus eine Symmetrieachse bestimmen. Um sie kann die Rotationsebene gekippt werden, ohne dass sich die Gesamtladung 0 verändert.
|
|
Eindeutigkeit
|
Die oben gefundene Anordnung der Schalen ist in Bezug auf den Erhalt der Ladung notwendig, denn jede Verletzung dieser Anordnung verletzt auch die Quantenzahl der Ladung.
|
|
|
Spin
|
Jetzt wird kontrolliert, inwieweit die Einhaltung des korrekten Spins die Freiheitsgrade der Oszi-Kreiswellen zusätzlich eingeschränkt.
|
|
|
Proton
Spin 1
(= ½ klassisch)
|
Der Spin der beiden Up-Oszis addiert sich zu 0, da sie in einer Ebene gegenläufig laufen. Übrig bleibt nur noch der Spin des Down-Oszis, der 1 beträgt! Die beiden fest verknüpften Up-Ebenen, die zusammenfallen, können sich dabei gemeinsam gegenüber der Down-Ebene verdrehen.
|
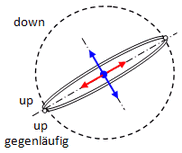 Abb. 1.2.3a Abb. 1.2.3a
Spin Proton = 1
Eingezeichnet sind
nur die Vektoren,
die sich zu 0 ergänzen!
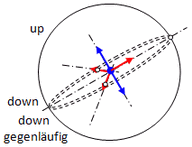 Abb. 1.2.3b Abb. 1.2.3b
Spin Neutron = 1
Eingezeichnet sind
nur die Vektoren,
die sich zu 0 ergänzen!
|
|
Satz 1.2.4
Aufbau Proton
|
Für die Bahnebenen der 2 Down-Oszis und des Up-Oszis gilt:
a) Die Bahnebene des Down-Oszis ist völlig frei.
b) Die Bahnen der beiden Up-Oszis laufen in einer Ebene gegenläufig,
wobei die gemeinsame Ebene in ihrer Lage zur Down-Ebene völlig frei ist.
|
|
Neutron
Spin 1
(= ½ klassisch)
|
Wenn sich der Spin der Down-Oszis gegenseitig auslöschen würde, wäre man fertig: Spin des Up-Oszi = Spin des Neutron = 1. Wird eine der beiden Down-Ebenen um die Symmetrieachse seiner Ladung gedreht, und zwar um 180°, so sind die Spin-Vektoren entgegengesetzt gerichtet. Da die Symmetrieachsen der Ladung nicht deckungsgleich sind, stellt dies die einzige Lösung dar. Für die Auslöschung ist es egal, welches der Down-Oszis gedreht wird. In jedem Fall sind damit die Drehrichtungen in der Down-Ebene gegenläufig, und da jetzt nur noch das Up-Oszi den Spin bestimmt, darf die Up-Ebene um die gemeinsame Symmetrieachse der Down-Ebene gedreht werden.
|
|
Satz 1.2.5
Aufbau Neutron
|
Für die Bahnebenen der 2 Down-Oszis und des Up-Oszis gilt:
a) Die Symmetrieachsen der Ladungen bilden in der Down-Ebene
ein symmetrisches Achsenkreuz (3 x 120°).
b) Die Bahnebene des Up-Oszis kann sich um die Symmetrieachse
seiner Ladung drehen.
|
|
Eindeutigkeit
|
Die nun gefundene Anordnung der Schalen ist in Bezug auf den Erhalt der Ladung und des Spins notwendig, denn jede Verletzung dieser Anordnung verletzt mindestens eine der beiden Quantenzahlen.
Achtung, die Überlegungen zur Orientierung der Schalen wurden unter der Prämisse angestellt, dass sich die Quanten nicht gegenseitig beeinflussen, womit die Eindeutigkeit erst mit dem Dilemma der QT gegeben ist!
- Punkt 1 ist damit gezeigt!
|
|
|
zu Punkt 2
|
Jetzt sollen die Massen vom Up- und Down-Oszi bestimmt werden. Auch wenn bei ihrer Berechnung auf die experimentell bekannten Massen von Proton und Neutron zurückgegriffen wird, führen ihre bekannten Strukturformeln allein nicht zum Ziel. Grund sind die Massendefekte, die bei der Kombination der Oszis zu Nukleonen auftreten. Um die zu bestimmen, muss auf den β-Zerfall zurückgegriffen werden. Aber selbst dann ist die Berechnung der Massen mathematisch noch unmöglich!
|
Berechnung der Massen
|
|
arithmetische
Symmetrie
|
Um die Berechnung überhaupt durchführen zu können, muss zusätzlich von folgender Symmetrie ausgegangen werden:
md = ms + me und mu = ms - me, womit md - mu = 2me gilt.
ms ist dabei die Masse der arithmetischen Symmetrie.
Auch wenn es damit eine weitere Unbekannte gibt, so ist sie im Netzwerk der einzuhaltenden Bedingungen eine freie Variable (Zielwertsuche).
|
mu, md = Massen von Up- und Down-Oszis,
me = Masse des Elektrons (bekannt)
|
|
|
Ausgehend von der arithmetischen Symmetrie ergibt sich die geometrische, die verallgemeinert zur allgemeinen Symmetrie wird. Mit ihr reicht zur Berechnung des Up- und Down-Oszis allein die Masse des Elektrons. Im Nachhinein rechtfertigt dies natürlich die Benutzung der arithmetischen Symmetrie. Andererseits ist sie auch so zu erkennen. Man rechne einfach mal ohne die Massendefekte, also nur aufgrund der Strukturformeln (falsch aber aufschlussreich).
|
- siehe Kapitel 2.1
|
|
Massendefekt
|
Sollen die Strukturgleichungen den Massendefekt berücksichtigen, so sind sie um die Massendefekte mp und mn zu ergänzen:
|
Korrektur um Massendefekte
|
|
β-Zerfall
|
Um die unbekannten Massendefekte mN und mP zu bestimmen, wird das Feynman-Diagramm des β-Zerfalls zu Rate gezogen.
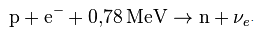
Um das Proton zu zerlegen, ist zumindest der Massendefekt an Energie zuzuführen. Auf der rechten Seite des Diagramms fehlt die kinetische Energie. Sie soll in der Masse mk stecken. Dann ist
2mu +md + mp + me + 1,39… 10-30 kg = mu+2md + mn + mk und
umgestellt mn - mp = me + 1,39… 10-30 kg - (md - mu) + mk,
mit md - mu = 2me (siehe arithmetische Symmetrie) folgt
mn - mp = 1,39… 10-30 kg - me + mk
|
Die Masse des Elektron-Neutrinos (0 oder > 0)
darf bei der Rechengenauigkeit von Excel vernachlässigt werden.
0,78 MeV entsprechen 1,39047623898693 10-30 kg
Für die fehlenden kinetischen Energien ergibt
sich damit 2,33329165995185 keV.
|
|
|
Die linke Seite der letzten Gleichung ist konstant. Die rechte Seite weist 3 Summanden auf, die für verschiedene Energieformen stehen. Diese Tatsache macht den Aufbau der Exceltabelle eindeutig (Physik).
|
- siehe Berechnung (Exceltabelle)
|
|
Berechnung der
arithmetischen
Symmetrie
|
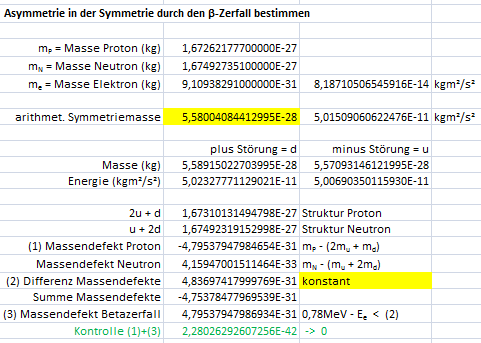
|
Ausgangswerte in der nebenstehenden Tabelle
sind die Masse des Protons, des Neutrons, des
Elektrons und die Lichtgeschwindigkeit c.
Zielwert war die arithmetische Symmetriemasse.
Der Zielwert wurde so bestimmt, dass der Wert
in der Kontrollzeile möglichst nahe bei 0 liegt.
|
|
|
Die Masse des Up- und Down-Oszis ergeben sich aus der arithmetischen Symmetriemasse durch Addition bzw. Subtraktion der Masse eines Elektrons, das die Störung darstellt.
- Punkt 2 ist damit abgearbeitet!
|
|
|
Tabelle
Up- und Down-Oszis
|
|
Oszi
|
Masse
10-28 kg
|
Energie
10-11 kgm²/s²
|
λ Compton
10-15 m
|
λ reduziert
10-15 m
|
Kreiswelle
|
|
Ladung
|
Spin
|
|
up
|
5,57093146122
|
5,02327771129
|
3,967413557719
|
5,230280515721
|
+1
|
+1
|
|
down
|
5,58915022704
|
5,02329017244
|
3,954481112610
|
5,213231545481
|
+1
|
+1
|
|
Achtung, der Spin ist in der TO nach Definition
doppelt so groß wie in der klassischen QM!
|
|
Kreiswellendurchmesser
|
Mit d = λ/π ergibt sich dann:
du = 1,66484999566855 10-15 und dd = 1,65942313989184 10-15 m
wobei λ = λ (1 + 1/π) ist.
|
Protondurchmesser schrumpft: Jetzt bei 1,68 Femtometer
(Science 25.1.13: Vol. 339 no. 6118 pp. 417).
|
|
Immer noch um 0,9% zu groß!
|
|
|
|
|
|
1.3
|
Oszi-Achten
|
letzte Änderung 26.01.2018
|
|
|
Die Modellvorstellung zum Aufbau von Proton und Neutron aus Up- und Down-Oszis ist noch nicht abgeschlossen. Es fehlt die Bindung untereinander, die über Oszi-Achten erfolgen soll. Da vorausgesetzt werden darf, dass sich Wellen nur stetig verbinden, gilt:
|
Die Oszi-Achten liefern eine erste Vorstellung davon,
was hinter der starken Wechselwirkung stecken könnte!
|
|
Satz 1.3.1
|
Ein Übergang von Oszis kann nur unter gleichen Oszis, in der gleichen Ebene
und unter Berücksichtigung der Phasenlage stattfinden.
|
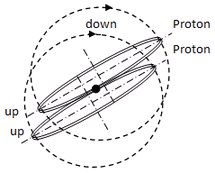
Abb. 1.3.1
doppelter
Übergang in
der Up-Ebene
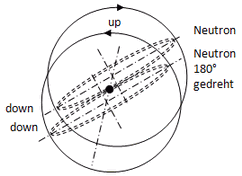
Abb. 1.3.2
doppelter
Übergang in
der Down-Ebene
|
|
|
Ohne die möglichen Andockpunkte im Einzelnen zu betrachten, geschieht das Andocken entweder über die Up- oder Down-Schalen. Die möglichen Andockpunkte verschieben sich mit der Phasenlage und wandern somit auf Meridianen über die Schalen.
Da Up- und doppelte Down-Ebene beim Proton nicht über die Phasenlage gekoppelt sind, wirkt dies wie ein Gelenk. Beim Neutron sind alle Kreiswellen über ihre Phasenlage fest verkoppelt, womit die Bindung versteifend wirkt.
|
|
doppelte Übergänge
|
Beim Proton betrifft dies die Up-Oszis, die in einer Ebene gegenläufig kreisen. Der Übergang ist auf dem gesamten Meridian möglich, da die Umkehrung der Drehrichtung einer Phasenverschiebung von 180° entspricht - siehe Abb. 1.3.1a.
Beim Neutron betrifft dies die Down-Oszis, die in einer Ebene gegenläufig kreisen. Bevor die Drehrichtung eines der Oszis gegenläufig wurde, betrug die ursprüngliche Phasenverschiebung 120°. Bei dieser Asymmetrie kann der Übergang in beiden Ebenen nur erfolgen, wenn das zweite Neutron auf den Kopf gedreht wird. Erfolgt die Drehung beim zweiten um die gemeinsame Symmetrieachse der Down-Ebene, liegt ein möglicher Übergang orthogonal dazu - siehe Abb. 1.3.1b. Die Phasenlage zueinander bleibt natürlich erhalten, wenn sich die zwei doppelten Down-Kreise gegeneinander abwälzen (wie Zahnräder).
|
|
Antiproton
|
Es lassen sich 4 Protonen über die Down-Oszis als Acht zu einem geschlossenen Zyklus verbinden. Die Mittelpunkte der Kreiswellen liegen dann auf den Eckpunkten eines Quadrates. Durch den Wechsel von links- zu rechtsdrehend und umgekehrt entsteht die folgende Sequenzen von Phasenverschiebungen:
|
|
|
Jede dritte Down-Kreiswelle ist dann wieder gleichläufig mit der ersten, und zwar ohne Phasenverschiebung (1/4π + 3/4π = 2π = 0 modulo 2π). Die Gegenläufigkeit ist äquivalent zu einer Phasenverschiebung um π. Eine diagonal verlaufende Oszi-Acht würde damit auf eine Auslöschung hinauslaufen. Also ist in dem Zyklus jedes Proton das fiktive Antiproton seines diagonal liegenden Partners.
|
Das Antiproton ist nur scheinbar
im Viererzyklus existent.
|
|
Bindung der Kernbausteine
|
Um damit weitermachen zu können, fehlen noch zwei wesentliche Dinge:
- Die qualitative und quantitative Erklärung der starken Wechselwirkung.
- Der Entwurf einer Bindungsalgebra, mit der die Packprobleme im Kern mittels eines Computermodells simuliert werden können.
|
Der letzte Punkt ist nicht Bestandteil dieses Beitrags.
|
|
EDM
|
Dies steht für das elektromagnetische Dipolmoment. Da die Packung der Atomkerne unter Minimierung der Gesamtmasse erfolgt, führt dies bei größeren Kernen zwangsläufig zu Geometrien, in welcher der Kern in seiner Gesamtheit einen elektromagnetischen Dipol bildet.
|
- siehe Kapitel 2 und 3
|
|
Überlegung
zur starken WW
|
Der gedankliche Versuch eine Oszi-Acht zu zerreißen, führt im nächsten Kapitel zur Entzauberung der starken Wechselwirkung. Entweder reißt sie - oder nicht, was auf einen Bernoulli-Versuch hinausläuft. Es ergibt sich die quadratintegrierbare Dichtefunktion der starken Wechselwirkung (sWW). Sie bestimmt die Stärke ihrer Wirkung als stetige Funktion in eineindeutiger Abhängigkeit von der Geometrie, womit Einstein wieder einmal recht behält - siehe rechts. Andererseits lässt sich die sWW aufgrund ihrer Herleitung als Instabilität deuten. Dabei geht es um die Energie, die noch zusätzlich aufzuwenden ist, um den String zu zerreißen: Das Fass zum Überlaufen bringt. Dennoch lässt sich kein direkter Zusammenhang zur Halbwertzeit beim radioaktiven Zerfall herstellen. So hat die relative Instabilität des freien Neutrons im Vergleich zum Proton primär ihre Ursache in der Verkopplung der Schalen und die damit verbundene Einschränkung der Freiheitsgrade bei der Impulsübertragung - siehe oben. Die Effektivität der Impulsübertragung spielt also eine entscheidende Rolle.
|
“Gott würfelt nicht!”
(Albert Einstein)
|